I have been working hard to solve the trigonometry issues with Euler rotations out of Poser normal vectors to align props to the surface of solids. Wow, that's a mouthful, isn't it? LOL
Disclaimer: In the following lines I will take you through a trip into the third and FOURTH dimensions. Not recommended for the weak of heart. Some things will turn to the Dark Side, where black holes, madness and some hysterical ladies live. You have been warned.
Many of the trigonometry "black holes" were covered, but we still have issues close to the equator, as seen below. As Y approaches zero at the equator, the trigonometry ladies go hysterical. What we see below is the visual explanation for why Euler rotations suck. I thought that solving the poles would be tough, but the equator seems even crazier. They should have been locked up at the Arkham Asylum long ago, but you know, they always manage to escape and come back to haunt us.
One could argue that this was supposed to be simple: I already have the normalized normal vectors, and all I need to do is convert them into Euler rotation angles. How hard could that be, right? If you have used Poser for long enough, you might have tried to orient the camera by dragging that ball on the left side - that's controlled by Euler rotations. When we get to right angles (the cardinal points), the camera freaks out and jumps to random places, apparently out of control. If you have tried that, you will understand why some sticks below go crazy, even when I am giving them the correct angles. Below I have solved the poles, but the equator still freaks out. Trigonometry seems so elegant and exact, but hey, it also goes crazy. Our teachers have rarely mentioned the madness behind calculating triangles, and how they can easily betray you by turning to the Dark Side. They look cute and cuddly at first , until you eventually face their true evil nature. Chaos rules even math! LOL
This is one of the reasons why math came up with "quaternion" rotations - they don't go crazy, but we have to tap into the 4th dimension to produce them. That's why they get that name (quat = 4). But hay, Poser only works in 3 dimensions, so how would a 4D rotation help? Well, a single quaternion indeed rotates in 4D, and cannot be used in 3D. But when we combine TWO quaternions, the intersection between them ends up joining one common axis, producing a gridlock-free 3D rotation! Hence the name "dual-quaternion" (DQ).
But Ken, isn't that just used in game engines, and the DS4 platform? Nope,
Poser has quaternion rotations as well! It just doesn't use them on the interface (because it hates you). So first the good news: DQ rotations are available through the Poser Python API. That's great, right? Yes, and now comes the bad news - the documentation is poor, leaving things to the imagination. DQ math uses linear algebra with matrices, and Python has wonderful libraries to do just that, but we can't use them in Poser because it uses it's own Python installation. We can't install libraries as far as I know. Even if I could, the library would only exist in my computer, so my code would only work here.
I am hence itching to switch to dual quaternions to get rid of the Euler rotation madness, which brings us closer to the Dark Side with lack of documentation and support. However, the Dark Side is very seductive, and sometimes it's hard to resist it.
If I can make it work on a sphere, it should work on any surface.
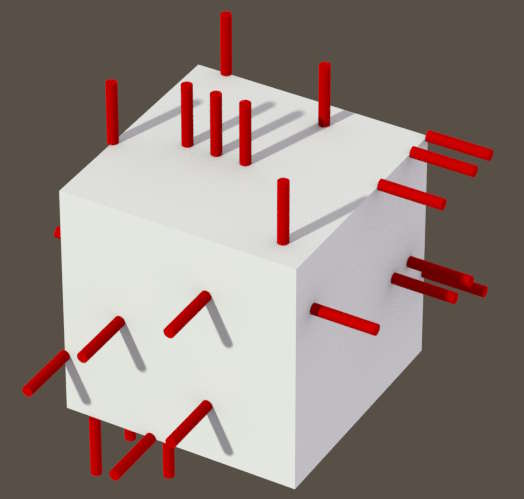
We can build entire 3D visualization systems with just linear algebra and trigonometry. My teachers never told me that when I learned that stuff back in the day. It would had been much more interesting and fun if I knew what it meant, and where it could be applied.
